Introduction
Dynamic Programming is an optimization approach where you divide the program into sub-problems whose results are reused to improve performance. Dynamic Programming helps avoid techniques like recursion, where repetitive calculations are present. It is like caching the results to be used later when required.

Fig: Dynamic programming example for Fibonacci problem | Credit: GeeksForGeeks
Optimal Substructure
Optimal Substructure means obtaining optimal solutions for a problem by finding optimal solutions for the smaller subproblems. For example, if we have a huge problem that can be divided into smaller subproblems, and if we find optimal solutions for those subproblems and curate the results for the final solution, we will reach the optimal solution for our main problem. Optimal Substructure also simplifies complex problems by breaking them into more manageable components.
Overlapping Subproblems
When you repeatedly encounter the same scenario while trying to solve a problem, it is referred to as overlapping subproblems in the problem-solving process. Instead of solving the same problem again and again, dynamic programming takes advantage of this repetition by solving each subproblem only once and storing its solution for future use.
Memoization and Tabulation
Memoization: In computer programming, memoization is an optimization technique that makes applications faster and more efficient. By storing or caching the results and retrieving the same information when required by the application, we can make applications quicker and more efficient. This can be used to speed up the execution of recursive functions by avoiding recomputation of the same subproblem multiple times.
Memoization is closely related to Overlapping Subproblems but there are some differences:

Fig: Difference between Memoization and Overlapping Subproblems in Dynamic Programming | Credit: Google Bard
Tabulation: A tabulation is a bottom-up approach that solves the problem by filling up a table with the solutions of the subproblems. This table is usually an array used to look up the values when required. Tabulation differs from memoization as it is useful when a problem can be divided into sequential steps or stages, and each stage is dependent only on its previous stage.
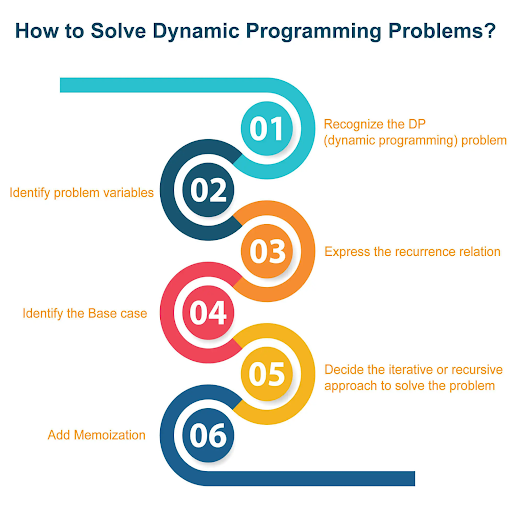
How to solve Dynamic Programming problems? | Credits: FavTutor
Real-Life Applications
Dynamic programming is a powerful technique that solves a wide variety of real-life problems, including:
- Finding Shortest Path: Navigation systems, transportation routing, network routing, and game pathfinding.
- Finding Knapsack Problems: Resource allocation and management, portfolio optimization, and project scheduling.
- Text Analysis: Spell checking, DNA sequence alignment, plagiarism detection.
- Decision Making: Robotics, autonomous vehicles, financial portfolio management, industrial process optimization.
- Economics and Game Theory: Auction design, pricing strategies, market equilibrium.
Conclusion
In the programming and problem-solving world Dynamic Programming emerges as a powerful method for optimizing performance. It introduces the concept of segregating intricate and complex challenges into smaller, solvable fragments, fostering efficiency through reusability. Optimal substructure and overlapping subproblems guide the process, enabling us to combine optimal solutions for smaller parts leading to optimal solutions for the whole. Using memoization (storing results of subproblems) and constructing solutions iteratively with tabulation, dynamic programming minimizes redundancy and maximizes efficiency. Dynamic Programming finds its place in diverse real-world scenarios, from guiding navigation systems and managing resources to analyzing text and enhancing decision-making.





